Regression Example#

This notebook provides two examples for performing basic regression on nonlinear data. The first example builds a traditional neural network and the second uses an affine observable PMM.

Imports#

[1]:

%pip install scikit-learn

Requirement already satisfied: scikit-learn in /home/pcook/Research/FRIB/pmmenv/lib/python3.12/site-packages (1.8.0)
Requirement already satisfied: numpy>=1.24.1 in /home/pcook/Research/FRIB/pmmenv/lib/python3.12/site-packages (from scikit-learn) (2.4.0)
Requirement already satisfied: scipy>=1.10.0 in /home/pcook/Research/FRIB/pmmenv/lib/python3.12/site-packages (from scikit-learn) (1.16.3)
Requirement already satisfied: joblib>=1.3.0 in /home/pcook/Research/FRIB/pmmenv/lib/python3.12/site-packages (from scikit-learn) (1.5.3)
Requirement already satisfied: threadpoolctl>=3.2.0 in /home/pcook/Research/FRIB/pmmenv/lib/python3.12/site-packages (from scikit-learn) (3.6.0)
Note: you may need to restart the kernel to use updated packages.

[2]:

import jax
import jax.numpy as np
import jax.random as jr
import parametricmatrixmodels as pmm
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, MinMaxScaler
# enable x64 for JAX
jax.config.update("jax_enable_x64", True)

Data Creation#

[3]:

# random seed for reproducibility
SEED = 0
key = jr.key(SEED)

n_pnts = 100
X = np.linspace(-2 * np.pi, 2 * np.pi, n_pnts)
Y = np.sin(X) + 0.1 * X**2

# add noise
key, noise_key = jr.split(key)

Y = Y + 0.2 * jr.normal(noise_key, Y.shape)

# data must be in the shape [n_pnts, n_features] for the pmm library
X = X[:, None]
Y = Y[:, None]
print(X.shape)
print(Y.shape)

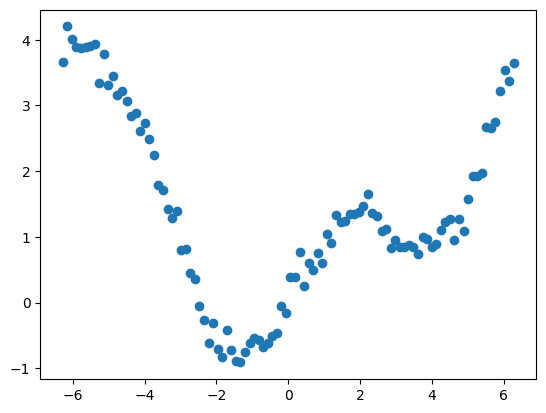
plt.plot(X, Y, 'o')

(100, 1)
(100, 1)

[3]:

[<matplotlib.lines.Line2D at 0x7683e6423d70>]

../_images/examples_basic_regression_5_2.png

Data Partitioning#

[4]:

# train on 70% of the data, validate on 15%, test on the rest
train_perc = 0.7
val_perc = 0.15

n_train = int(n_pnts * train_perc)
n_val = int(n_pnts * val_perc)
n_test = n_pnts - n_train - n_val

key, shuffle_key = jr.split(key)

# shuffle the data and then split
X_sh = jr.permutation(shuffle_key, X)
Y_sh = jr.permutation(shuffle_key, Y)

X_train = X_sh[:n_train]
Y_train = Y_sh[:n_train]
X_val = X_sh[n_train:n_train + n_val]
Y_val = Y_sh[n_train:n_train + n_val]
X_test = X_sh[n_train + n_val:]
Y_test = Y_sh[n_train + n_val:]

Traditional Neural Network#

Data Preparation (Scaling)#

Regression neural networks typically function best when the data are scaled to have unit variance and zero mean (StandardScaler)

[5]:

xscaler = StandardScaler()
yscaler = StandardScaler()

X_train_sc = xscaler.fit_transform(X_train)
X_val_sc = xscaler.transform(X_val)
Y_train_sc = yscaler.fit_transform(Y_train)
Y_val_sc = yscaler.transform(Y_val)

# we need to convert the arrays back from numpy arrays to jax.numpy arrays, since sklearn uses pure numpy
X_train_sc = np.array(X_train_sc)
X_val_sc = np.array(X_val_sc)
Y_train_sc = np.array(Y_train_sc)
Y_val_sc = np.array(Y_val_sc)

Model Creation#

The model is built from an ordered sequence of Modules. For a traditional neural network, these are just LinearNN modules. Since we want linear sequential execution, we use a SequentialModel.

[6]:

# two hidden layers with 64 neurons each and the ReLU activation function
# one output neuron
modules = [
        pmm.modules.LinearNN(
            out_features=64, bias=True, activation=pmm.modules.ReLU()
        ),
        pmm.modules.LinearNN(
            out_features=64, bias=True, activation=pmm.modules.ReLU()
        ),
        pmm.modules.LinearNN(out_features=1, bias=True),
    ]

model = pmm.SequentialModel(modules)

# print model summary before compilation
print(model)

SequentialModel(
  [
   LinearNN(
     []
   ),
   LinearNN(
     []
   ),
   LinearNN(
     []
   ),
  ]
)

We can see that the model summary is very sparse at the moment. This is because the model doesn’t know what data to expect yet and doesn’t have any initial values for trainable parameters.

Model Compilation#

It’s more accurate to call this preparation or initialization, since all compilation happens JIT. This step doesn’t need to be done manually, as the model will automatically compile itself for the provided training data when the Model.train method is called.

Models are compiled by providing them with a random key or seed as well as the shape of the input data (excluding the batch dimension). This allows the model to prepare all its modules by, for instance, setting initial values for trainable parameters. Forward passes (inferences/predictions) cannot be done with Models (or Modules) until after compilation with the corresponding input shape.

[7]:

key, compile_key = jr.split(key)

# the random key here can be replaced with an integer seed or None, in which case a random seed will be chosen
# the model only needs to know the input shape without the batch dimension
model.compile(key, X_train_sc.shape[1:])

# print the model summary after compilation
print(model)
print(f"Total trainable floats: {model.get_num_trainable_floats()}")

SequentialModel(
  [
   LinearNN(
     [
      Flatten,
      MatMul(trainable) (trainable floats: 64),
      Bias(real=True) (trainable floats: 64),
      ReLU,
     ]
   ),
   LinearNN(
     [
      Flatten,
      MatMul(trainable) (trainable floats: 4,096),
      Bias(real=True) (trainable floats: 64),
      ReLU,
     ]
   ),
   LinearNN(
     [
      Flatten,
      MatMul(trainable) (trainable floats: 64),
      Bias(real=True) (trainable floats: 1),
     ]
   ),
  ]
)
Total trainable floats: 4353

Now we see some actual details about the model. We can see it is built from 3 LinearNN Modules (which themselves are actually also Models) which use three to four submodules each: Flatten, a trainable MatMul, a trainable and real-valued Bias, and for the hidden layers ReLU. This represents the classic \(f(Wx+b)\) neural network layer operation.

We can perform a forward pass (inference/prediction) with the randomly initialized model just to make sure everything is working:

[8]:

model(np.array([[1.0]]))

[8]:

Array([[-0.00960011]], dtype=float64)

64-bit versus 32-bit#

By default, JAX disables 64-bit floating point support (double precision). This is re-enabled by calling jax.config.update("jax_enable_x64", True) after JAX is imported but before it is initialized (usually before the first array operation). On certain hardware (like consumer GPUs) 64-bit operations can be nearly an order of magnitude slower than 32-bit. Additionally, there is little benefit to storing the trainable parameters of a model in 64-bit precision or for training models with 64-bit precision. It is for this reason that the PMM library defaults to (and will raise warnings otherwise) 32-bit models, 32-bit training, and 64-bit inference.

Here, we explicitly cast the model to 32-bit as well as the training/validation data.

[9]:

model = model.astype(np.float32)

X_train_sc_32 = X_train_sc.astype(np.float32)
Y_train_sc_32 = Y_train_sc.astype(np.float32)
X_val_sc_32 = X_val_sc.astype(np.float32)
Y_val_sc_32 = Y_val_sc.astype(np.float32)

Training#

To train the model, we simply call the model.train() method and supply it with the training and validation data and optionally things like the loss function and options for the optimization process such as the learning rate, total number of epochs, batch size, etc.

[10]:

key, batch_key = jr.split(key)

model.train(
    X_train_sc_32,
    Y=Y_train_sc_32,
    X_val=X_val_sc_32,
    Y_val=Y_val_sc_32,
    lr=1e-2,
    epochs=250,
    batch_size=5,
    batch_rng=batch_key,
    verbose=True)

1/250 | 7.8607e-01/7.8607e-01 [####################] (0s)
2/250 | 5.0318e-01/5.0318e-01 [####################] (0s)
3/250 | 4.5940e-01/4.5940e-01 [####################] (0s)
4/250 | 4.0544e-01/4.0544e-01 [####################] (0s)
5/250 | 3.6005e-01/3.6005e-01 [####################] (0s)
6/250 | 2.8516e-01/2.8516e-01 [####################] (0s)
7/250 | 2.5043e-01/2.5043e-01 [####################] (0s)
8/250 | 2.2804e-01/2.2804e-01 [####################] (0s)
9/250 | 1.9864e-01/1.9864e-01 [####################] (0s)
10/250 | 1.8128e-01/1.8128e-01 [####################] (0s)
11/250 | 1.8519e-01/1.8128e-01 [####################] (0s)
12/250 | 1.6765e-01/1.6765e-01 [####################] (0s)
13/250 | 1.5993e-01/1.5993e-01 [####################] (0s)
14/250 | 1.5118e-01/1.5118e-01 [####################] (0s)
15/250 | 1.4756e-01/1.4756e-01 [####################] (0s)
16/250 | 1.4488e-01/1.4488e-01 [####################] (0s)
17/250 | 1.5423e-01/1.4488e-01 [####################] (0s)
18/250 | 1.3836e-01/1.3836e-01 [####################] (0s)
19/250 | 1.2858e-01/1.2858e-01 [####################] (0s)
20/250 | 1.3492e-01/1.2858e-01 [####################] (0s)
21/250 | 1.2824e-01/1.2824e-01 [####################] (0s)
22/250 | 1.2356e-01/1.2356e-01 [####################] (0s)
23/250 | 1.1941e-01/1.1941e-01 [####################] (0s)
24/250 | 1.3161e-01/1.1941e-01 [####################] (0s)
25/250 | 1.2221e-01/1.1941e-01 [####################] (0s)
26/250 | 1.2183e-01/1.1941e-01 [####################] (0s)
27/250 | 1.1759e-01/1.1759e-01 [####################] (0s)
28/250 | 1.1619e-01/1.1619e-01 [####################] (0s)
29/250 | 1.1807e-01/1.1619e-01 [####################] (0s)
30/250 | 1.0958e-01/1.0958e-01 [####################] (0s)
31/250 | 1.3600e-01/1.0958e-01 [####################] (0s)
32/250 | 1.1083e-01/1.0958e-01 [####################] (0s)
33/250 | 1.0806e-01/1.0806e-01 [####################] (0s)
34/250 | 1.1257e-01/1.0806e-01 [####################] (0s)
35/250 | 1.2772e-01/1.0806e-01 [####################] (0s)
36/250 | 1.1246e-01/1.0806e-01 [####################] (0s)
37/250 | 1.0966e-01/1.0806e-01 [####################] (0s)
38/250 | 1.2023e-01/1.0806e-01 [####################] (0s)
39/250 | 1.0668e-01/1.0668e-01 [####################] (0s)
40/250 | 1.0356e-01/1.0356e-01 [####################] (0s)
41/250 | 1.1708e-01/1.0356e-01 [####################] (0s)
42/250 | 1.0925e-01/1.0356e-01 [####################] (0s)
43/250 | 1.0966e-01/1.0356e-01 [####################] (0s)
44/250 | 1.0242e-01/1.0242e-01 [####################] (0s)
45/250 | 1.0997e-01/1.0242e-01 [####################] (0s)
46/250 | 1.0356e-01/1.0242e-01 [####################] (0s)
47/250 | 1.0313e-01/1.0242e-01 [####################] (0s)
48/250 | 1.0253e-01/1.0242e-01 [####################] (0s)
49/250 | 1.0032e-01/1.0032e-01 [####################] (0s)
50/250 | 9.7897e-02/9.7897e-02 [####################] (0s)
51/250 | 1.0216e-01/9.7897e-02 [####################] (0s)
52/250 | 1.0057e-01/9.7897e-02 [####################] (0s)
53/250 | 1.0118e-01/9.7897e-02 [####################] (0s)
54/250 | 9.7351e-02/9.7351e-02 [####################] (0s)
55/250 | 1.1234e-01/9.7351e-02 [####################] (0s)
56/250 | 9.3110e-02/9.3110e-02 [####################] (0s)
57/250 | 9.9734e-02/9.3110e-02 [####################] (0s)
58/250 | 9.1770e-02/9.1770e-02 [####################] (0s)
59/250 | 8.9069e-02/8.9069e-02 [####################] (0s)
60/250 | 1.0289e-01/8.9069e-02 [####################] (0s)
61/250 | 9.6913e-02/8.9069e-02 [####################] (0s)
62/250 | 9.6241e-02/8.9069e-02 [####################] (0s)
63/250 | 9.8420e-02/8.9069e-02 [####################] (0s)
64/250 | 8.7649e-02/8.7649e-02 [####################] (0s)
65/250 | 9.0070e-02/8.7649e-02 [####################] (0s)
66/250 | 9.6413e-02/8.7649e-02 [####################] (0s)
67/250 | 9.2351e-02/8.7649e-02 [####################] (0s)
68/250 | 1.0716e-01/8.7649e-02 [####################] (0s)
69/250 | 1.0409e-01/8.7649e-02 [####################] (0s)
70/250 | 8.6707e-02/8.6707e-02 [####################] (0s)
71/250 | 8.8159e-02/8.6707e-02 [####################] (0s)
72/250 | 8.7628e-02/8.6707e-02 [####################] (0s)
73/250 | 8.3547e-02/8.3547e-02 [####################] (0s)
74/250 | 8.0006e-02/8.0006e-02 [####################] (0s)
75/250 | 8.8055e-02/8.0006e-02 [####################] (0s)
76/250 | 8.6013e-02/8.0006e-02 [####################] (0s)
77/250 | 9.0464e-02/8.0006e-02 [####################] (0s)
78/250 | 8.8312e-02/8.0006e-02 [####################] (0s)
79/250 | 8.0211e-02/8.0006e-02 [####################] (0s)
80/250 | 8.8458e-02/8.0006e-02 [####################] (0s)
81/250 | 8.6534e-02/8.0006e-02 [####################] (0s)
82/250 | 8.5332e-02/8.0006e-02 [####################] (0s)
83/250 | 8.3566e-02/8.0006e-02 [####################] (0s)
84/250 | 8.0716e-02/8.0006e-02 [####################] (0s)
85/250 | 8.1569e-02/8.0006e-02 [####################] (0s)
86/250 | 8.0372e-02/8.0006e-02 [####################] (0s)
87/250 | 7.9148e-02/7.9148e-02 [####################] (0s)
88/250 | 7.3478e-02/7.3478e-02 [####################] (0s)
89/250 | 8.1903e-02/7.3478e-02 [####################] (0s)
90/250 | 1.0176e-01/7.3478e-02 [####################] (0s)
91/250 | 8.8403e-02/7.3478e-02 [####################] (0s)
92/250 | 9.1995e-02/7.3478e-02 [####################] (0s)
93/250 | 1.0767e-01/7.3478e-02 [####################] (0s)
94/250 | 8.3559e-02/7.3478e-02 [####################] (0s)
95/250 | 7.8728e-02/7.3478e-02 [####################] (0s)
96/250 | 7.3051e-02/7.3051e-02 [####################] (0s)
97/250 | 9.4739e-02/7.3051e-02 [####################] (0s)
98/250 | 9.4280e-02/7.3051e-02 [####################] (0s)
99/250 | 9.2930e-02/7.3051e-02 [####################] (0s)
100/250 | 7.2277e-02/7.2277e-02 [####################] (0s)
101/250 | 7.1439e-02/7.1439e-02 [####################] (0s)
102/250 | 6.8890e-02/6.8890e-02 [####################] (0s)
103/250 | 6.8998e-02/6.8890e-02 [####################] (0s)
104/250 | 7.1708e-02/6.8890e-02 [####################] (0s)
105/250 | 7.4463e-02/6.8890e-02 [####################] (0s)
106/250 | 6.4985e-02/6.4985e-02 [####################] (0s)
107/250 | 6.9123e-02/6.4985e-02 [####################] (0s)
108/250 | 6.5660e-02/6.4985e-02 [####################] (0s)
109/250 | 6.5931e-02/6.4985e-02 [####################] (0s)
110/250 | 6.1449e-02/6.1449e-02 [####################] (0s)
111/250 | 6.4720e-02/6.1449e-02 [####################] (0s)
112/250 | 6.7240e-02/6.1449e-02 [####################] (0s)
113/250 | 7.3970e-02/6.1449e-02 [####################] (0s)
114/250 | 6.1726e-02/6.1449e-02 [####################] (0s)
115/250 | 8.1460e-02/6.1449e-02 [####################] (0s)
116/250 | 8.6221e-02/6.1449e-02 [####################] (0s)
117/250 | 7.0352e-02/6.1449e-02 [####################] (0s)
118/250 | 7.6675e-02/6.1449e-02 [####################] (0s)
119/250 | 9.5870e-02/6.1449e-02 [####################] (0s)
120/250 | 8.7505e-02/6.1449e-02 [####################] (0s)
121/250 | 8.1257e-02/6.1449e-02 [####################] (0s)
122/250 | 8.4181e-02/6.1449e-02 [####################] (0s)
123/250 | 7.5042e-02/6.1449e-02 [####################] (0s)
124/250 | 6.2688e-02/6.1449e-02 [####################] (0s)
125/250 | 8.3008e-02/6.1449e-02 [####################] (0s)
126/250 | 6.0585e-02/6.0585e-02 [####################] (0s)
127/250 | 6.7834e-02/6.0585e-02 [####################] (0s)
128/250 | 9.3002e-02/6.0585e-02 [####################] (0s)
129/250 | 8.4863e-02/6.0585e-02 [####################] (0s)
130/250 | 6.4601e-02/6.0585e-02 [####################] (0s)
131/250 | 6.9106e-02/6.0585e-02 [####################] (0s)
132/250 | 6.9529e-02/6.0585e-02 [####################] (0s)
133/250 | 6.9735e-02/6.0585e-02 [####################] (0s)
134/250 | 6.3158e-02/6.0585e-02 [####################] (0s)
135/250 | 5.8077e-02/5.8077e-02 [####################] (0s)
136/250 | 5.8051e-02/5.8051e-02 [####################] (0s)
137/250 | 5.1926e-02/5.1926e-02 [####################] (0s)
138/250 | 6.9325e-02/5.1926e-02 [####################] (0s)
139/250 | 6.6578e-02/5.1926e-02 [####################] (0s)
140/250 | 5.4720e-02/5.1926e-02 [####################] (0s)
141/250 | 6.1397e-02/5.1926e-02 [####################] (0s)
142/250 | 4.6176e-02/4.6176e-02 [####################] (0s)
143/250 | 5.6338e-02/4.6176e-02 [####################] (0s)
144/250 | 5.9826e-02/4.6176e-02 [####################] (0s)
145/250 | 5.2593e-02/4.6176e-02 [####################] (0s)
146/250 | 4.7631e-02/4.6176e-02 [####################] (0s)
147/250 | 6.0039e-02/4.6176e-02 [####################] (0s)
148/250 | 5.1952e-02/4.6176e-02 [####################] (0s)
149/250 | 6.4384e-02/4.6176e-02 [####################] (0s)
150/250 | 4.7902e-02/4.6176e-02 [####################] (0s)
151/250 | 5.4240e-02/4.6176e-02 [####################] (0s)
152/250 | 8.7593e-02/4.6176e-02 [####################] (0s)
153/250 | 5.5680e-02/4.6176e-02 [####################] (0s)
154/250 | 5.9909e-02/4.6176e-02 [####################] (0s)
155/250 | 4.5948e-02/4.5948e-02 [####################] (0s)
156/250 | 4.5787e-02/4.5787e-02 [####################] (0s)
157/250 | 5.4487e-02/4.5787e-02 [####################] (0s)
158/250 | 4.5993e-02/4.5787e-02 [####################] (0s)
159/250 | 5.2104e-02/4.5787e-02 [####################] (0s)
160/250 | 6.5566e-02/4.5787e-02 [####################] (0s)
161/250 | 4.5222e-02/4.5222e-02 [####################] (0s)
162/250 | 5.6127e-02/4.5222e-02 [####################] (0s)
163/250 | 5.9438e-02/4.5222e-02 [####################] (0s)
164/250 | 4.9327e-02/4.5222e-02 [####################] (0s)
165/250 | 3.8123e-02/3.8123e-02 [####################] (0s)
166/250 | 5.3154e-02/3.8123e-02 [####################] (0s)
167/250 | 4.5029e-02/3.8123e-02 [####################] (0s)
168/250 | 4.1853e-02/3.8123e-02 [####################] (0s)
169/250 | 4.6038e-02/3.8123e-02 [####################] (0s)
170/250 | 5.9997e-02/3.8123e-02 [####################] (0s)
171/250 | 4.2596e-02/3.8123e-02 [####################] (0s)
172/250 | 4.8706e-02/3.8123e-02 [####################] (0s)
173/250 | 4.2727e-02/3.8123e-02 [####################] (0s)
174/250 | 5.2578e-02/3.8123e-02 [####################] (0s)
175/250 | 4.3788e-02/3.8123e-02 [####################] (0s)
176/250 | 7.0637e-02/3.8123e-02 [####################] (0s)
177/250 | 4.1196e-02/3.8123e-02 [####################] (0s)
178/250 | 3.1865e-02/3.1865e-02 [####################] (0s)
179/250 | 3.7221e-02/3.1865e-02 [####################] (0s)
180/250 | 3.3198e-02/3.1865e-02 [####################] (0s)
181/250 | 3.1750e-02/3.1750e-02 [####################] (0s)
182/250 | 3.2191e-02/3.1750e-02 [####################] (0s)
183/250 | 3.5275e-02/3.1750e-02 [####################] (0s)
184/250 | 5.1212e-02/3.1750e-02 [####################] (0s)
185/250 | 4.9963e-02/3.1750e-02 [####################] (0s)
186/250 | 4.9463e-02/3.1750e-02 [####################] (0s)
187/250 | 5.6674e-02/3.1750e-02 [####################] (0s)
188/250 | 2.8552e-02/2.8552e-02 [####################] (0s)
189/250 | 2.9090e-02/2.8552e-02 [####################] (0s)
190/250 | 2.9629e-02/2.8552e-02 [####################] (0s)
191/250 | 3.5665e-02/2.8552e-02 [####################] (0s)
192/250 | 3.7032e-02/2.8552e-02 [####################] (0s)
193/250 | 2.9679e-02/2.8552e-02 [####################] (0s)
194/250 | 3.8773e-02/2.8552e-02 [####################] (0s)
195/250 | 3.4265e-02/2.8552e-02 [####################] (0s)
196/250 | 4.1550e-02/2.8552e-02 [####################] (0s)
197/250 | 3.5000e-02/2.8552e-02 [####################] (0s)
198/250 | 3.6903e-02/2.8552e-02 [####################] (0s)
199/250 | 2.7838e-02/2.7838e-02 [####################] (0s)
200/250 | 2.5960e-02/2.5960e-02 [####################] (0s)
201/250 | 2.7936e-02/2.5960e-02 [####################] (0s)
202/250 | 3.4787e-02/2.5960e-02 [####################] (0s)
203/250 | 3.4081e-02/2.5960e-02 [####################] (0s)
204/250 | 4.0938e-02/2.5960e-02 [####################] (0s)
205/250 | 3.7885e-02/2.5960e-02 [####################] (0s)
206/250 | 3.4678e-02/2.5960e-02 [####################] (0s)
207/250 | 6.0238e-02/2.5960e-02 [####################] (0s)
208/250 | 3.5822e-02/2.5960e-02 [####################] (0s)
209/250 | 2.8570e-02/2.5960e-02 [####################] (0s)
210/250 | 2.7827e-02/2.5960e-02 [####################] (0s)
211/250 | 3.3676e-02/2.5960e-02 [####################] (0s)
212/250 | 3.0658e-02/2.5960e-02 [####################] (0s)
213/250 | 3.1736e-02/2.5960e-02 [####################] (0s)
214/250 | 3.2551e-02/2.5960e-02 [####################] (0s)
215/250 | 2.3595e-02/2.3595e-02 [####################] (0s)
216/250 | 3.0965e-02/2.3595e-02 [####################] (0s)
217/250 | 4.1416e-02/2.3595e-02 [####################] (0s)
218/250 | 7.1400e-02/2.3595e-02 [####################] (0s)
219/250 | 6.0360e-02/2.3595e-02 [####################] (0s)
220/250 | 4.7201e-02/2.3595e-02 [####################] (0s)
221/250 | 4.6297e-02/2.3595e-02 [####################] (0s)
222/250 | 4.8735e-02/2.3595e-02 [####################] (0s)
223/250 | 3.6821e-02/2.3595e-02 [####################] (0s)
224/250 | 3.1825e-02/2.3595e-02 [####################] (0s)
225/250 | 3.2482e-02/2.3595e-02 [####################] (0s)
226/250 | 3.4695e-02/2.3595e-02 [####################] (0s)
227/250 | 3.2790e-02/2.3595e-02 [####################] (0s)
228/250 | 3.5002e-02/2.3595e-02 [####################] (0s)
229/250 | 4.2969e-02/2.3595e-02 [####################] (0s)
230/250 | 4.6462e-02/2.3595e-02 [####################] (0s)
231/250 | 4.0521e-02/2.3595e-02 [####################] (0s)
232/250 | 3.8239e-02/2.3595e-02 [####################] (0s)
233/250 | 3.0208e-02/2.3595e-02 [####################] (0s)
234/250 | 2.4054e-02/2.3595e-02 [####################] (0s)
235/250 | 4.7296e-02/2.3595e-02 [####################] (0s)
236/250 | 3.9185e-02/2.3595e-02 [####################] (0s)
237/250 | 3.4520e-02/2.3595e-02 [####################] (0s)
238/250 | 3.4001e-02/2.3595e-02 [####################] (0s)
239/250 | 4.1196e-02/2.3595e-02 [####################] (0s)
240/250 | 2.8311e-02/2.3595e-02 [####################] (0s)
241/250 | 5.0485e-02/2.3595e-02 [####################] (0s)
242/250 | 3.6910e-02/2.3595e-02 [####################] (0s)
243/250 | 4.3837e-02/2.3595e-02 [####################] (0s)
244/250 | 3.7291e-02/2.3595e-02 [####################] (0s)
245/250 | 3.3454e-02/2.3595e-02 [####################] (0s)
246/250 | 2.1437e-02/2.1437e-02 [####################] (0s)
247/250 | 3.5610e-02/2.1437e-02 [####################] (0s)
248/250 | 2.7829e-02/2.1437e-02 [####################] (0s)
249/250 | 4.2877e-02/2.1437e-02 [####################] (0s)
250/250 | 3.8412e-02/2.1437e-02 [####################] (0s)

========================================
Total epochs: 250
(best epoch: 245)
(best validation loss: 2.1437E-02)
========================================

Inference#

Now we’re ready to make new predictions with the model. All Models and Modules are directly callable once compiled, so we need only to pass in the (scaled) inputs like model(X) and unscale the predictions.

[11]:

# pass in the scaled inputs (converted to JAX arrays again)
X_sc = xscaler.transform(X)
X_sc = np.array(X_sc)

# get scaled predictions
Y_pred_sc = model(X_sc)

# unscale predictions
Y_pred = yscaler.inverse_transform(Y_pred_sc)

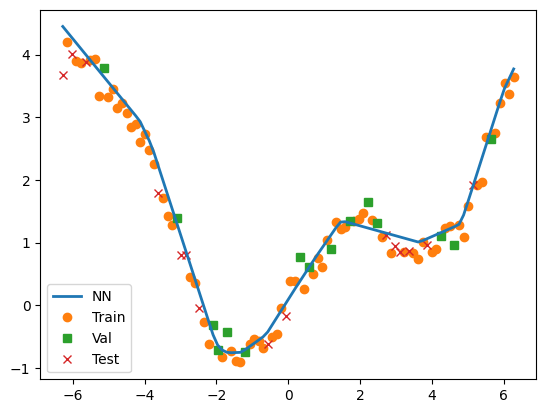
# plot results
plt.plot(X, Y_pred, label="NN", lw=2, zorder=10)
plt.plot(X_train, Y_train, 'o', label="Train")
plt.plot(X_val, Y_val, 's', label="Val")
plt.plot(X_test, Y_test, 'x', label="Test")
plt.legend()

[11]:

<matplotlib.legend.Legend at 0x7683987c4cb0>

../_images/examples_basic_regression_23_1.png

Parametric Matrix Model (`AffineObservablePMM`)#

Here we repeat the above process for the AffineObservablePMM, which is both a Module and a Model. For consistency, we wrap it with a SequentialModel, though this isn’t necessary as it is itself a subclass of SequentialModel. The only other difference in usage here is that this kind of PMM performs best when the data are scaled uniformly, using MinMaxScaler.

Data Preparation (Scaling)#

This kind of PMM typically functions best when the data are scaled uniformly (MinMaxScaler)

[12]:

xscaler = MinMaxScaler()
yscaler = MinMaxScaler()

X_train_sc = xscaler.fit_transform(X_train)
X_val_sc = xscaler.transform(X_val)
Y_train_sc = yscaler.fit_transform(Y_train)
Y_val_sc = yscaler.transform(Y_val)

# we need to convert the arrays back from numpy arrays to jax.numpy arrays, since sklearn uses pure numpy
X_train_sc = np.array(X_train_sc)
X_val_sc = np.array(X_val_sc)
Y_train_sc = np.array(Y_train_sc)
Y_val_sc = np.array(Y_val_sc)

Model Creation#

This model is a single AffineObservablePMM module with a Hermitian matrices size of 5, two eigenvectors, one secondary matrix, and using expectation values instead of transition amplitudes. Internally, this Module is just a SequentialModel of Modules that first form the primary matrix \(H(c) = H_0 + \sum_i c_i H_i\), then take the eigendecomposition, then compute the sum of transition amplitudes or expectation values with trainable secondary matrices, then finally add a trainable bias.

[13]:

# just a single PMM module, which contains all the submodules
modules = [
        pmm.modules.AffineObservablePMM(
            matrix_size=5,
            num_eig=2,
            num_secondaries=1,
            output_size=1,
            use_expectation_values=True
        )
    ]

model = pmm.SequentialModel(modules)

# print model summary before compilation
print(model)
print(f"Total trainable floats: {model.get_num_trainable_floats()}")

SequentialModel(
  [
   AffineObservablePMM(
     []
   ),
  ]
)
Total trainable floats: 0

We can see that the model summary is very sparse at the moment. This is because the model doesn’t know what data to expect yet and doesn’t have any initial values for trainable parameters.

Model Compilation#

[14]:

key, compile_key = jr.split(key)

# the random key here can be replaced with an integer seed or None, in which case a random seed will be chosen
# the model only needs to know the input shape without the batch dimension
model.compile(key, X_train_sc.shape[1:])

# print the model summary after compilation
print(model)

SequentialModel(
  [
   AffineObservablePMM(
     (
      AffineHermitianMatrix(5x5,) (trainable floats: 50),
      Eigenvectors(num_eig=2, which=LM),
      ExpectationValueSum(output_size=1, num_observables=1, centered=True) (trainable floats: 25),
      Bias(real=True) (trainable floats: 1),
     )
   ),
  ]
)

Now we see some actual details about the model. We can see it is built from 1 AffineObservablePMM Module (which itself is a Model) which uses four submodules: AffineHermitianMatrix, Eigenvectors, ExpectationValueSum, and Bias.

We can perform a forward pass (inference/prediction) with the randomly initialized model just to make sure everything is working:

[15]:

model(np.array([[1.0]]))

[15]:

Array([[0.01202144]], dtype=float64)

64-bit versus 32-bit#

Here, we explicitly cast the model to 32-bit as well as the training/validation data.

[16]:

model = model.astype(np.float32)

X_train_sc_32 = X_train_sc.astype(np.float32)
Y_train_sc_32 = Y_train_sc.astype(np.float32)
X_val_sc_32 = X_val_sc.astype(np.float32)
Y_val_sc_32 = Y_val_sc.astype(np.float32)

Training#

[17]:

# using the same batch key as with the neural network
model.train(
    X_train_sc_32,
    Y=Y_train_sc_32,
    X_val=X_val_sc_32,
    Y_val=Y_val_sc_32,
    lr=1e-2,
    epochs=250,
    batch_size=5,
    batch_rng=batch_key,
    verbose=True)

1/250 | 5.4442e-02/5.4442e-02 [####################] (0s)
2/250 | 1.1614e-01/5.4442e-02 [####################] (0s)
3/250 | 5.6446e-02/5.4442e-02 [####################] (0s)
4/250 | 5.8632e-02/5.4442e-02 [####################] (0s)
5/250 | 9.0178e-02/5.4442e-02 [####################] (0s)
6/250 | 5.4176e-02/5.4176e-02 [####################] (0s)
7/250 | 6.2531e-02/5.4176e-02 [####################] (0s)
8/250 | 5.2981e-02/5.2981e-02 [####################] (0s)
9/250 | 3.3681e-02/3.3681e-02 [####################] (0s)
10/250 | 2.9399e-02/2.9399e-02 [####################] (0s)
11/250 | 3.0416e-02/2.9399e-02 [####################] (0s)
12/250 | 2.5683e-02/2.5683e-02 [####################] (0s)
13/250 | 2.2098e-02/2.2098e-02 [####################] (0s)
14/250 | 1.8719e-02/1.8719e-02 [####################] (0s)
15/250 | 1.2611e-02/1.2611e-02 [####################] (0s)
16/250 | 1.0284e-02/1.0284e-02 [####################] (0s)
17/250 | 1.0085e-02/1.0085e-02 [####################] (0s)
18/250 | 1.2628e-02/1.0085e-02 [####################] (0s)
19/250 | 8.1678e-03/8.1678e-03 [####################] (0s)
20/250 | 6.8490e-03/6.8490e-03 [####################] (0s)
21/250 | 7.4929e-03/6.8490e-03 [####################] (0s)
22/250 | 6.5267e-03/6.5267e-03 [####################] (0s)
23/250 | 5.5787e-03/5.5787e-03 [####################] (0s)
24/250 | 7.4365e-03/5.5787e-03 [####################] (0s)
25/250 | 6.4864e-03/5.5787e-03 [####################] (0s)
26/250 | 6.3493e-03/5.5787e-03 [####################] (0s)
27/250 | 5.9987e-03/5.5787e-03 [####################] (0s)
28/250 | 7.7315e-03/5.5787e-03 [####################] (0s)
29/250 | 5.9036e-03/5.5787e-03 [####################] (0s)
30/250 | 6.0343e-03/5.5787e-03 [####################] (0s)
31/250 | 6.7738e-03/5.5787e-03 [####################] (0s)
32/250 | 6.3439e-03/5.5787e-03 [####################] (0s)
33/250 | 9.1537e-03/5.5787e-03 [####################] (0s)
34/250 | 7.5088e-03/5.5787e-03 [####################] (0s)
35/250 | 6.0626e-03/5.5787e-03 [####################] (0s)
36/250 | 6.4997e-03/5.5787e-03 [####################] (0s)
37/250 | 6.7489e-03/5.5787e-03 [####################] (0s)
38/250 | 7.2865e-03/5.5787e-03 [####################] (0s)
39/250 | 7.4852e-03/5.5787e-03 [####################] (0s)
40/250 | 6.1094e-03/5.5787e-03 [####################] (0s)
41/250 | 5.7489e-03/5.5787e-03 [####################] (0s)
42/250 | 6.0052e-03/5.5787e-03 [####################] (0s)
43/250 | 7.0590e-03/5.5787e-03 [####################] (0s)
44/250 | 7.0230e-03/5.5787e-03 [####################] (0s)
45/250 | 6.9031e-03/5.5787e-03 [####################] (0s)
46/250 | 6.2807e-03/5.5787e-03 [####################] (0s)
47/250 | 7.0101e-03/5.5787e-03 [####################] (0s)
48/250 | 7.6631e-03/5.5787e-03 [####################] (0s)
49/250 | 6.0248e-03/5.5787e-03 [####################] (0s)
50/250 | 6.5716e-03/5.5787e-03 [####################] (0s)
51/250 | 6.7445e-03/5.5787e-03 [####################] (0s)
52/250 | 5.2785e-03/5.2785e-03 [####################] (0s)
53/250 | 3.1016e-03/3.1016e-03 [####################] (0s)
54/250 | 8.9250e-03/3.1016e-03 [####################] (0s)
55/250 | 6.9021e-03/3.1016e-03 [####################] (0s)
56/250 | 3.8885e-03/3.1016e-03 [####################] (0s)
57/250 | 7.6216e-03/3.1016e-03 [####################] (0s)
58/250 | 7.3961e-03/3.1016e-03 [####################] (0s)
59/250 | 7.0220e-03/3.1016e-03 [####################] (0s)
60/250 | 6.1720e-03/3.1016e-03 [####################] (0s)
61/250 | 5.7947e-03/3.1016e-03 [####################] (0s)
62/250 | 5.0734e-03/3.1016e-03 [####################] (0s)
63/250 | 4.9879e-03/3.1016e-03 [####################] (0s)
64/250 | 5.5361e-03/3.1016e-03 [####################] (0s)
65/250 | 4.5192e-03/3.1016e-03 [####################] (0s)
66/250 | 6.7327e-03/3.1016e-03 [####################] (0s)
67/250 | 7.7463e-03/3.1016e-03 [####################] (0s)
68/250 | 5.5338e-03/3.1016e-03 [####################] (0s)
69/250 | 3.7159e-03/3.1016e-03 [####################] (0s)
70/250 | 3.1470e-03/3.1016e-03 [####################] (0s)
71/250 | 5.3691e-03/3.1016e-03 [####################] (0s)
72/250 | 9.9612e-03/3.1016e-03 [####################] (0s)
73/250 | 5.4284e-03/3.1016e-03 [####################] (0s)
74/250 | 6.3011e-03/3.1016e-03 [####################] (0s)
75/250 | 4.0493e-03/3.1016e-03 [####################] (0s)
76/250 | 4.3772e-03/3.1016e-03 [####################] (0s)
77/250 | 4.2802e-03/3.1016e-03 [####################] (0s)
78/250 | 6.9974e-03/3.1016e-03 [####################] (0s)
79/250 | 3.5675e-03/3.1016e-03 [####################] (0s)
80/250 | 5.5649e-03/3.1016e-03 [####################] (0s)
81/250 | 7.4596e-03/3.1016e-03 [####################] (0s)
82/250 | 4.3281e-03/3.1016e-03 [####################] (0s)
83/250 | 2.9820e-03/2.9820e-03 [####################] (0s)
84/250 | 6.6735e-03/2.9820e-03 [####################] (0s)
85/250 | 3.7156e-03/2.9820e-03 [####################] (0s)
86/250 | 2.8052e-03/2.8052e-03 [####################] (0s)
87/250 | 1.6796e-02/2.8052e-03 [####################] (0s)
88/250 | 1.0363e-02/2.8052e-03 [####################] (0s)
89/250 | 5.0196e-03/2.8052e-03 [####################] (0s)
90/250 | 3.4737e-03/2.8052e-03 [####################] (0s)
91/250 | 1.9751e-03/1.9751e-03 [####################] (0s)
92/250 | 2.8802e-03/1.9751e-03 [####################] (0s)
93/250 | 5.8319e-03/1.9751e-03 [####################] (0s)
94/250 | 3.4529e-03/1.9751e-03 [####################] (0s)
95/250 | 2.6395e-03/1.9751e-03 [####################] (0s)
96/250 | 2.8948e-03/1.9751e-03 [####################] (0s)
97/250 | 3.9332e-03/1.9751e-03 [####################] (0s)
98/250 | 5.2598e-03/1.9751e-03 [####################] (0s)
99/250 | 4.5422e-03/1.9751e-03 [####################] (0s)
100/250 | 3.1950e-03/1.9751e-03 [####################] (0s)
101/250 | 7.2841e-03/1.9751e-03 [####################] (0s)
102/250 | 7.1810e-03/1.9751e-03 [####################] (0s)
103/250 | 5.0848e-03/1.9751e-03 [####################] (0s)
104/250 | 3.0136e-03/1.9751e-03 [####################] (0s)
105/250 | 2.4440e-03/1.9751e-03 [####################] (0s)
106/250 | 3.4854e-03/1.9751e-03 [####################] (0s)
107/250 | 3.3913e-03/1.9751e-03 [####################] (0s)
108/250 | 1.9056e-03/1.9056e-03 [####################] (0s)
109/250 | 2.3935e-03/1.9056e-03 [####################] (0s)
110/250 | 2.2171e-03/1.9056e-03 [####################] (0s)
111/250 | 2.8577e-03/1.9056e-03 [####################] (0s)
112/250 | 2.0798e-03/1.9056e-03 [####################] (0s)
113/250 | 2.2106e-03/1.9056e-03 [####################] (0s)
114/250 | 2.2582e-03/1.9056e-03 [####################] (0s)
115/250 | 1.9352e-03/1.9056e-03 [####################] (0s)
116/250 | 3.8784e-03/1.9056e-03 [####################] (0s)
117/250 | 2.3278e-03/1.9056e-03 [####################] (0s)
118/250 | 6.5267e-03/1.9056e-03 [####################] (0s)
119/250 | 7.0995e-03/1.9056e-03 [####################] (0s)
120/250 | 2.6266e-03/1.9056e-03 [####################] (0s)
121/250 | 4.7335e-03/1.9056e-03 [####################] (0s)
122/250 | 7.1512e-03/1.9056e-03 [####################] (0s)
123/250 | 4.2358e-03/1.9056e-03 [####################] (0s)
124/250 | 3.5876e-03/1.9056e-03 [####################] (0s)
125/250 | 3.0308e-03/1.9056e-03 [####################] (0s)
126/250 | 4.3498e-03/1.9056e-03 [####################] (0s)
127/250 | 3.6074e-03/1.9056e-03 [####################] (0s)
128/250 | 3.4459e-03/1.9056e-03 [####################] (0s)
129/250 | 2.9632e-03/1.9056e-03 [####################] (0s)
130/250 | 3.1751e-03/1.9056e-03 [####################] (0s)
131/250 | 3.5406e-03/1.9056e-03 [####################] (0s)
132/250 | 2.7615e-03/1.9056e-03 [####################] (0s)
133/250 | 2.3193e-03/1.9056e-03 [####################] (0s)
134/250 | 2.5355e-03/1.9056e-03 [####################] (0s)
135/250 | 2.2808e-03/1.9056e-03 [####################] (0s)
136/250 | 2.4032e-03/1.9056e-03 [####################] (0s)
137/250 | 3.0431e-03/1.9056e-03 [####################] (0s)
138/250 | 2.8142e-03/1.9056e-03 [####################] (0s)
139/250 | 1.9903e-03/1.9056e-03 [####################] (0s)
140/250 | 1.9782e-03/1.9056e-03 [####################] (0s)
141/250 | 1.9603e-03/1.9056e-03 [####################] (0s)
142/250 | 2.7303e-03/1.9056e-03 [####################] (0s)
143/250 | 5.9771e-03/1.9056e-03 [####################] (0s)
144/250 | 4.0507e-03/1.9056e-03 [####################] (0s)
145/250 | 2.1805e-03/1.9056e-03 [####################] (0s)
146/250 | 1.7523e-03/1.7523e-03 [####################] (0s)
147/250 | 2.2935e-03/1.7523e-03 [####################] (0s)
148/250 | 3.1664e-03/1.7523e-03 [####################] (0s)
149/250 | 3.0230e-03/1.7523e-03 [####################] (0s)
150/250 | 2.4747e-03/1.7523e-03 [####################] (0s)
151/250 | 3.7523e-03/1.7523e-03 [####################] (0s)
152/250 | 5.4125e-03/1.7523e-03 [####################] (0s)
153/250 | 2.5811e-03/1.7523e-03 [####################] (0s)
154/250 | 4.2159e-03/1.7523e-03 [####################] (0s)
155/250 | 3.1262e-03/1.7523e-03 [####################] (0s)
156/250 | 1.7317e-03/1.7317e-03 [####################] (0s)
157/250 | 4.1367e-03/1.7317e-03 [####################] (0s)
158/250 | 4.9401e-03/1.7317e-03 [####################] (0s)
159/250 | 7.3494e-03/1.7317e-03 [####################] (0s)
160/250 | 3.3021e-03/1.7317e-03 [####################] (0s)
161/250 | 4.1837e-03/1.7317e-03 [####################] (0s)
162/250 | 2.0441e-03/1.7317e-03 [####################] (0s)
163/250 | 2.8287e-03/1.7317e-03 [####################] (0s)
164/250 | 3.9031e-03/1.7317e-03 [####################] (0s)
165/250 | 3.3648e-03/1.7317e-03 [####################] (0s)
166/250 | 2.8648e-03/1.7317e-03 [####################] (0s)
167/250 | 2.1758e-03/1.7317e-03 [####################] (0s)
168/250 | 1.5925e-03/1.5925e-03 [####################] (0s)
169/250 | 2.4283e-03/1.5925e-03 [####################] (0s)
170/250 | 2.0659e-03/1.5925e-03 [####################] (0s)
171/250 | 2.6633e-03/1.5925e-03 [####################] (0s)
172/250 | 2.4290e-03/1.5925e-03 [####################] (0s)
173/250 | 3.4595e-03/1.5925e-03 [####################] (0s)
174/250 | 4.2879e-03/1.5925e-03 [####################] (0s)
175/250 | 2.5606e-03/1.5925e-03 [####################] (0s)
176/250 | 1.7552e-03/1.5925e-03 [####################] (0s)
177/250 | 1.8150e-03/1.5925e-03 [####################] (0s)
178/250 | 1.8843e-03/1.5925e-03 [####################] (0s)
179/250 | 2.4673e-03/1.5925e-03 [####################] (0s)
180/250 | 2.7264e-03/1.5925e-03 [####################] (0s)
181/250 | 6.2605e-03/1.5925e-03 [####################] (0s)
182/250 | 2.2474e-03/1.5925e-03 [####################] (0s)
183/250 | 5.4456e-03/1.5925e-03 [####################] (0s)
184/250 | 6.7805e-03/1.5925e-03 [####################] (0s)
185/250 | 5.3535e-03/1.5925e-03 [####################] (0s)
186/250 | 2.3965e-03/1.5925e-03 [####################] (0s)
187/250 | 4.7688e-03/1.5925e-03 [####################] (0s)
188/250 | 3.9332e-03/1.5925e-03 [####################] (0s)
189/250 | 2.9458e-03/1.5925e-03 [####################] (0s)
190/250 | 2.7969e-03/1.5925e-03 [####################] (0s)
191/250 | 3.7599e-03/1.5925e-03 [####################] (0s)
192/250 | 2.3289e-03/1.5925e-03 [####################] (0s)
193/250 | 2.3922e-03/1.5925e-03 [####################] (0s)
194/250 | 1.4419e-03/1.4419e-03 [####################] (0s)
195/250 | 1.7286e-03/1.4419e-03 [####################] (0s)
196/250 | 2.6265e-03/1.4419e-03 [####################] (0s)
197/250 | 5.1592e-03/1.4419e-03 [####################] (0s)
198/250 | 2.0504e-03/1.4419e-03 [####################] (0s)
199/250 | 1.8579e-03/1.4419e-03 [####################] (0s)
200/250 | 5.1812e-03/1.4419e-03 [####################] (0s)
201/250 | 5.8354e-03/1.4419e-03 [####################] (0s)
202/250 | 3.6949e-03/1.4419e-03 [####################] (0s)
203/250 | 2.4144e-03/1.4419e-03 [####################] (0s)
204/250 | 2.9960e-03/1.4419e-03 [####################] (0s)
205/250 | 4.1210e-03/1.4419e-03 [####################] (0s)
206/250 | 6.0538e-03/1.4419e-03 [####################] (0s)
207/250 | 5.2219e-03/1.4419e-03 [####################] (0s)
208/250 | 3.7427e-03/1.4419e-03 [####################] (0s)
209/250 | 4.7810e-03/1.4419e-03 [####################] (0s)
210/250 | 5.7836e-03/1.4419e-03 [####################] (0s)
211/250 | 2.9323e-03/1.4419e-03 [####################] (0s)
212/250 | 3.8641e-03/1.4419e-03 [####################] (0s)
213/250 | 4.2803e-03/1.4419e-03 [####################] (0s)
214/250 | 2.0412e-03/1.4419e-03 [####################] (0s)
215/250 | 1.6764e-03/1.4419e-03 [####################] (0s)
216/250 | 2.0434e-03/1.4419e-03 [####################] (0s)
217/250 | 3.2198e-03/1.4419e-03 [####################] (0s)
218/250 | 7.8106e-03/1.4419e-03 [####################] (0s)
219/250 | 3.3164e-03/1.4419e-03 [####################] (0s)
220/250 | 3.7824e-03/1.4419e-03 [####################] (0s)
221/250 | 4.9126e-03/1.4419e-03 [####################] (0s)
222/250 | 7.0033e-03/1.4419e-03 [####################] (0s)
223/250 | 7.2956e-03/1.4419e-03 [####################] (0s)
224/250 | 5.2377e-03/1.4419e-03 [####################] (0s)
225/250 | 3.7460e-03/1.4419e-03 [####################] (0s)
226/250 | 7.7423e-03/1.4419e-03 [####################] (0s)
227/250 | 9.5499e-03/1.4419e-03 [####################] (0s)
228/250 | 2.0417e-02/1.4419e-03 [####################] (0s)
229/250 | 7.7284e-03/1.4419e-03 [####################] (0s)
230/250 | 6.8024e-03/1.4419e-03 [####################] (0s)
231/250 | 6.3797e-03/1.4419e-03 [####################] (0s)
232/250 | 5.5671e-03/1.4419e-03 [####################] (0s)
233/250 | 5.5593e-03/1.4419e-03 [####################] (0s)
234/250 | 7.8933e-03/1.4419e-03 [####################] (0s)
235/250 | 1.3514e-02/1.4419e-03 [####################] (0s)
236/250 | 1.0794e-02/1.4419e-03 [####################] (0s)
237/250 | 5.7856e-03/1.4419e-03 [####################] (0s)
238/250 | 2.7149e-03/1.4419e-03 [####################] (0s)
239/250 | 2.0554e-03/1.4419e-03 [####################] (0s)
240/250 | 3.3540e-03/1.4419e-03 [####################] (0s)
241/250 | 5.6794e-03/1.4419e-03 [####################] (0s)
242/250 | 3.3093e-03/1.4419e-03 [####################] (0s)
243/250 | 3.2271e-03/1.4419e-03 [####################] (0s)
244/250 | 3.0530e-03/1.4419e-03 [####################] (0s)
245/250 | 1.7806e-03/1.4419e-03 [####################] (0s)
246/250 | 1.5051e-03/1.4419e-03 [####################] (0s)
247/250 | 3.2142e-03/1.4419e-03 [####################] (0s)
248/250 | 2.2576e-03/1.4419e-03 [####################] (0s)
249/250 | 1.9008e-03/1.4419e-03 [####################] (0s)
250/250 | 2.2744e-03/1.4419e-03 [####################] (0s)

========================================
Total epochs: 250
(best epoch: 193)
(best validation loss: 1.4419E-03)
========================================

Inference#

[18]:

# pass in the scaled inputs (converted to JAX arrays again)
X_sc = xscaler.transform(X)
X_sc = np.array(X_sc)

# get scaled predictions
Y_pred_sc = model(X_sc)

# unscale predictions
Y_pred = yscaler.inverse_transform(Y_pred_sc)

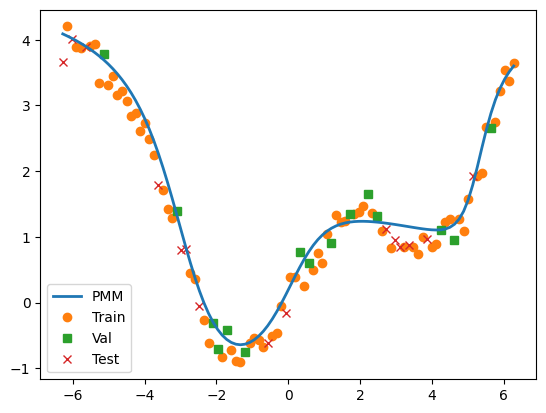
# plot results
plt.plot(X, Y_pred, label="PMM", lw=2, zorder=10)
plt.plot(X_train, Y_train, 'o', label="Train")
plt.plot(X_val, Y_val, 's', label="Val")
plt.plot(X_test, Y_test, 'x', label="Test")
plt.legend()

[18]:

<matplotlib.legend.Legend at 0x76838c619f70>

../_images/examples_basic_regression_39_1.png

Regression Example#

Imports#

Data Creation#

Data Partitioning#

Traditional Neural Network#

Data Preparation (Scaling)#

Model Creation#

Model Compilation#

64-bit versus 32-bit#

Training#

Inference#

Parametric Matrix Model (AffineObservablePMM)#

Data Preparation (Scaling)#

Model Creation#

Model Compilation#

64-bit versus 32-bit#

Training#

Inference#

This Page

Parametric Matrix Model (`AffineObservablePMM`)#